Hello everyone! I recently had the wonderful opportunity to shadow Dr. Arturo Perez from the University of Houston at Clear Lake in his classes Intro to IT and Forensic Fundamentals. I’m excited to share what I learned with you today!
A little background about Professor Perez. Dr. Arturo Perez is a lecturer in the College of Science and Engineering. Dr. Perez received his Ph.D. in Information Technology from Capella University in Minneapolis, Minnesota. He has a Master’s in Business Administration and Healthcare Management and a Bachelor of Science in Information Technology from The University of Phoenix.
In the Intro to IT class, I learned about the different numbering systems. Most of us are familiar with the decimal system, which uses numbers 0-9. However, other systems like binary and hexadecimal represent numbers differently.
Understanding the Binary System
The binary numbering system uses only 0 and 1, with 0 representing false/off and 1 representing true/on. Each position in a binary number has a place value that is a power of 2.
Binary to Decimal Conversion
To convert a binary number to decimal, you need to understand the position of each bit (binary digit). The rightmost bit is in the 0th place, and the place value increases by 1 as you move to the left.
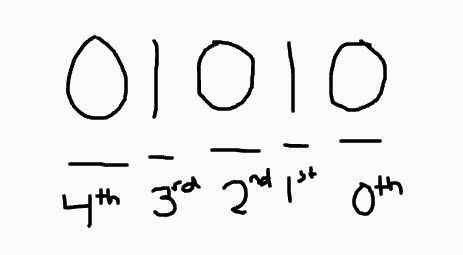
To convert from binary to decimal, you must raise 2 to the power of the places in which there is a 1. That sounds a little confusing, so let me give you an example. For the binary 01010101, you can see that there are 1s at the 0th, 2nd, 4th, and 6th place. Therefore, you must do 2^0 + 2^2 + 2^4 + 2^6. This equals 85, which is the decimal equivalent of 01010101.
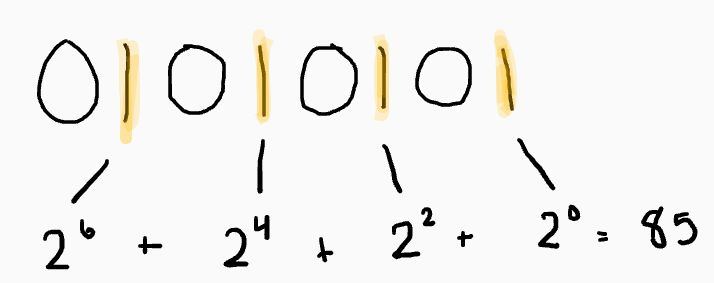
Decimal to Binary Conversion
Here I will be converting the decimal number 13 to binary.
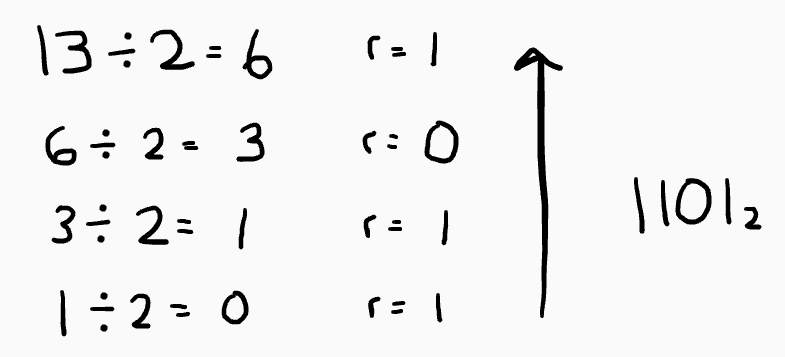
Start with the decimal number, and then divide this by 2. Write down the quotient, which is 6, and then the remainder, which is 1. Repeat this by continuing to divide the quotient by 2 and writing down the remainder to the side. Stop whenever the quotient is 0. Then, the answer is the remainders read from the bottom to the top, which is 1101. The subscript of 2 is to indicate what base the number is in. When there is no subscript it can be assumed that the number is in base 10, or the decimal system.
Summary
- Binary to decimal: identify positions with 1s, calculate 2^position, then sum them up
- Decimal to binary: divide by 2, write down remainders, then read from bottom to top.

Conclusion
I hope that this helps you understand numbering systems better and how to convert between them! Thanks to Dr. Perez’s classes, I’ve gained valuable insights into these fundamental concepts and I’m excited to share more with you in the future!
